Commentaires
Eliott
19 Sep. 2018, 18:06
C'est intéressant de voir les différences de prévisions suivant les
organisations. on rajoute votre site à notre section "bourse", une façon de
vous remercier pour la qualité de vos publications et de vos statistiques
article ici
Gauriot
22 Fév. 2018, 09:47
Comment peut on penser que l'inflation serai pour 2018 de 1.3% alors que
tout augmente (carburants impôts transports gaz électricité assurance
alimentation) dans des proportions de 2 à 7% dans la vie de tout les jours,
cela arrange sans doute le gouvernement qui n'est pas obligé d'augmenter
les pensions indexées. ces élites nous considère sans doute incapable de
calculer !!!!
Sylvie
23 Jan. 2017, 09:41
Bonjour, vous ne faites plus de prévisions depuis 2011 ? ce serait
intéressant d'avoir une prévision pour 2017, on pourrait justement en
parler sur notre site.
article ici .
kandin
21 Août 2016, 09:32
Bonjour
pouvez-vous me calculer le taux d'inflation entre 1er avril 2013 au 1er
avril 2016 ainsi que la formule detaillée
article ici
merci d'avance j-c kandin
OUEDRAOGO
24 Mars 2016, 15:18
Pourrais-je avoir de la documentation sur le modèle de prévision de l'ipc
utilisé sur ce site?
merci d'avance
Inflation Moyenne 2015
10 Déc. 2015, 16:08
L'inflation moyenne de 2015 ne sera pas de 0.6% selon la moyenne des
prévisions des organismes financiers en décembre 2014 : dans un mois, elle
s'avèrera nulle ! ...
ils prévoyaient même 1.1% en octobre 2014 !
cela révèle un sérieux manque de compétence, de clairvoyance ou, plus
grave encore, de sincérité de la part de ces acteurs professionnels de la
finance.
Prévisions Inflation
19 Oct. 2015, 17:59
Bien le bonjour.
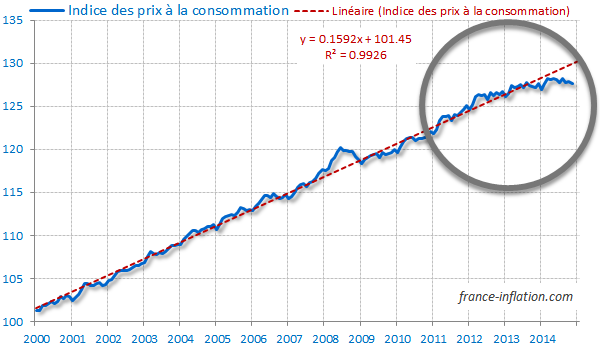
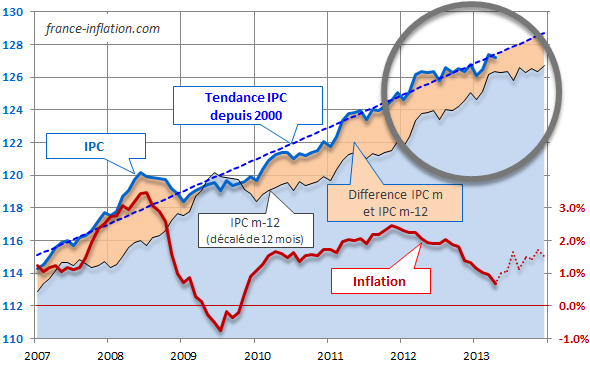
jusqu’en novembre 2014, la courbe de l’ipcm suit
approximativement, en passant alternativement au-dessus et au-dessous, sa
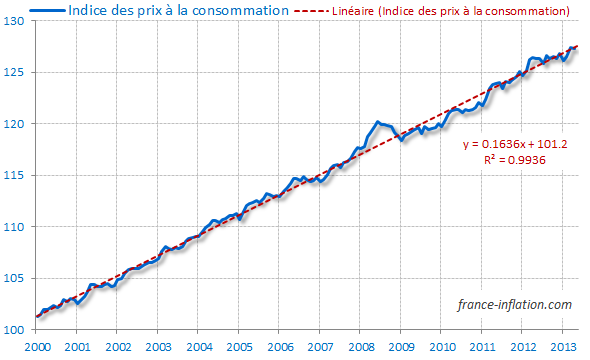
droite de tendance de base janvier 2000 et d’équation : y =
0.1592m+101.45.
on peut considérer qu’elle reste la plupart du temps dans un couloir
de tendance d’une largeur forfaitaire correspondant à l’ipcm ±
2.
1) en se plaçant en novembre 2014 : (cercle gris)
dans ce premier cas, pendant les derniers mois, la courbe moyenne de
l’ipcm se rapproche d’une ligne horizontale (inflation nulle)
elle sort, à la baisse, du couloir de tendance en octobre 2014, suite à une
série de variations au-dessous de sa droite de tendance depuis août 2013,
effectivement, d’où l’analyse prospective, bien fondée, du
phénomène qui s’est produit en à peine plus d’un an (14 mois),
intitulée : "les prévisions pour 2015 et 2016 vont être assez délicates".
2) en se plaçant en juin 2008 :
dans ce deuxième cas, pendant les derniers mois, la courbe moyenne de
l’ipcm se rapproche d’une ligne verticale (inflation
galopante)
elle sort, à la hausse, du couloir de tendance en mai 2008, suite à une
série de variations au-dessus de la droite de tendance depuis août 2007.
quelles auraient pu être les conclusions à attendre d’une analyse,
semblable à la précédente, de ce phénomène d’emballement encore plus
rapide (il n’avait suffi, alors, que de 9 mois !) ? ; sans la
connaissance, bien évidemment du futur de l’époque !
sincères salutations.
IPC Linéaire 8
30 Déc. 2014, 09:22
Bien le bonjour.
À l'attention de Mathématicien qui considère que 0.02 est proche de 0 et
que celà lui permet d'arrondir l'expression ln(1+t) à t :
Puisque, par ailleurs , quand il s'agit de chercher un taux d'inflation, il
introduit dans son raisonnement un taux d'intérêt qu'il semble maîtriser,
je lui suggère de considérer deux emprunts du même montant de 1M¤, par
exemple,remboursables par mensualités constantes sur la durée disons d'une
vie humaine de 80 ans (trois fois rien par rapport à l'éternité !), sans
autre coût que celui du montant des intérêts, le premier à un taux de 0% (=
0) , le second à un taux de 2% (= 0.02, proche de 0 selon lui ! ...)
Je pense qu'il saura constater que dans le premier cas le coût du prêt est
nul (= 0¤) et que dans le second il est supérieur à 1M¤, c'est à dire au
capital emprunté, et donc, pour pousser le bouchon un peu loin, une
infinité de fois plus que dans le premier cas ! ... Alors arrondir 0.02 à 0
?! ...
Tout ce raisonnement pour montrer qu'arrondir peut emmener à des résultats
aberrants : on peut faire dire n'importe quoi aux arrondis !
Sincères salutations.
IPC Linéaire 7
25 Déc. 2014, 21:34
Bien le bonjour.
Concernant l'intervention du 14/12/2014 : Non, la solution exacte de
(1+t)^x == 1+ix n'est pas t(x) = ((1+ix)^(1/x)-1 car on ne peut pas écrire
l'identification d'une foncion exponentielle avec une fonction linéaire !
(Voir mon post IPC Linéaire 6 de ce jour)
Je suis désolé de devoir à nouveau contredire Mathématicien qui tient tant
à passer par les logarithmes pour traiter la fonction exponentielle, mais
ici on n'a pas de fonction exponentielle contrairement au cas où le taux
est constant (Il est variable et, on est bien d'accord, décroissant : Nos
avis divergent juste sur la valeur de cette décroissance !)
Sincères salutations.
IPC Linéaire 6
25 Déc. 2014, 19:20
Bien le bonjour.
Concernant l'intervention du 13/12/2014, alors qu'il y est précisé, en
conclusion, que le taux est DÉCROISSANT, d'où l'intitulé "Taux décroissant"
pris par son auteur, il est vraiment curieux que ce dernier maintienne son
hypothèse non démontrée (et d'ailleurs non démontrable puisque fausse !
...) à savoir l'identité :
(1 + t)^x == 1 + i0 x.
En effet, l'exponentiation, dans le membre de gauche, est en fait ni plus
ni moins que l'élévation d'un terme donné CONSTANT (ici : la parenthèse) à
une puissance particulière (ici : x), c'est à dire la multiplication de ce
terme par lui-même x fois (oui, je sais, celà peut paraître bizarre quand x
n'est pas entier, mais c'est ainsi !)
Si t varie en fonction de x (et donc, n'est pas constant !), sur 10 ans par
exemple, tout au plus peut-on utiliser une expression du genre :
(1+t0)(1+t1)(1+t2)...(1+t9) ou
(1+t1)(1+t2)(1+t3)...(1+t10)
selon l'indice attribué à t pour l'année n.
Du coup, la fonction exponentielle disparait miraculeusement !
De toute façon, compte tenu du fait que toute fonction exponentielle en x
"l'emporte sur toute puissance de x ou tout polynôme en x quel que soit son
degré", il est absolument impossible de l'identifier à une fonction du
premier degré comme celle du second membre !
L'identification toute simple d'une fonction avec sa fonction carrée ne
peut déjà pas s'écrire, alors avec une fonction exponentielle ! ...
On peut, par exemple, écrire l'égalité (l'équation du second degré) x^2 = x
dont les solutions, x=0 et x=1, sont évidentes, sachant qu'aucune autre
valeur de x ne satisfait cette égalité.
x^2 n'est pas identique à x (sinon celà se saurait !) : On ne peut donc pas
écrire l'identité x^2 == x.
Il en va de même avec (1+t)^x == 1+i0 x !
L'hypothèse étant abusive, le raisonnement qui en découle est mal fondé et
les résultats qui en résultent pour le moins contestables !
Sincères salutations.
mathématicien
14 Déc. 2014, 11:50
Effectivement, la solution exacte de l'équation (1+ t)^x ==1+i.x est bien:
t[x]=((1+i.x)^(1/x))-1
On retrouve l'expression t = ln(1 + i.x)/x indiquée le 01/06/2013 en
utilisant la fonction log:
(1+ t)^x = 1+i.x
=> x.ln (1 + t) = ln(1 + i.x)
=> ln (1 + t) = ln (1 + i.x) / x
puis, par approximation:
~ t = ln (1 + i.x) / x
car ln (1 + t) ~ t pour t=0,02 proche de 0.
Taux décroissant
13 Déc. 2014, 15:26
La droite présentée peut s'écrire de manière simplifiée en partant d'un
indice qui vaut au temps x=0,f[x]= 1+ i0 x, avec i0=0.02 et x le temps qui
passe.
Soit t le taux variable recherché tel que (1+ t)^x ==1+io x.
La solution est t[x]=((1+i0 x)^(1/x))-1.
t[x] doit décroître très lentement de la manière suivante (exemple pour
i0=0.02 sur 10 ans)
{0.02, 0.0198039, 0.0196128, 0.0194265, 0.0192449, 0.0190676,0.0188946,
0.0187257, 0.0185606, 0.0183994}
Prévisions Inflation Moyenne 2014
07 Oct. 2014, 10:44
Bonjour
Ah, que voilà une prévision moyenne pour l'année 2014 bien plus raisonnable
de la part des organismes financiers ! :
0.7% d'Inflation alors qu'ils espéraient (incantaient ?) précédemment 1.4%,
soit tout de même 2 fois plus, donc une erreur de 100% ... si la nouvelle
prévision se réalise ! ...
Salutations
IPC Linéaire 5
06 Oct. 2014, 11:55
Bien le bonjour
Je remonte à l’origine de ce qui a déclenché mon intervention sur ce
site, à savoir l’affirmation de
Mathématicien le 01 Juin 2013, 14:06, quant à la
Réponse à la question du "coin des experts"
"Trouver la variation du taux d'inflation permettant une évolution linéaire
des prix"
Solution :
"Soit i le taux d'inflation, le taux d'intérêt t doit évoluer selon la
relation suivante en fonction de la période n:
t = ln(1 + i.n)/n (ln = log népérien)"
Sa solution, sans démonstration, comporte en elle-même une contradiction
qu’il ne semble pas déceler :
1) Il est demandé la formule de variation du Taux d’Inflation ;
2) Mathématicien nomme ce dernier "i" ;
3) Et il formule un Taux d’Intérêt ( ?), t, en fonction de i.
Donc :
Soit Mathématicien ne répond pas à la question posée, en ne donnant pas la
formule de i,
Soit, s’il pense y répondre, sa réponse est erronée ou incomplète
car, dans sa formule de t, i est non encore défini, puisque c’est lui
que l’on recherche !
Sincères salutations.
Prévisions Inflation Moyenne 2013-2014
05 Oct. 2014, 09:55
Bonjour
Comment croire les prévisions des banques, même moyennes :
2013 : Prévu 1%, Constaté 0.9%; soit une erreur de 10%!
2014 : prévu 1.4%, Constaté pour l'instant, sur 8 mois (au 2/3 de l'année):
Maxi=0.78%, mini =0.62% (Actuellement)
Il faudrait un sacré rebondissement pour que la moyenne atteigne la
prévision; ce n'est pas dans l'air du temps !
Si l'on arrive à nouveau à 0.9% ce sera déjà bien.
Et l'erreur serait alors de plus de 50% : une paille !
Et il ne s'agit que de moyennes !
Salutations
IPC Linéaire 4
04 Oct. 2014, 15:45
Bien le bonjour
Tout d’abord, sincèrement, merci à Mathématicien pour avoir repris le
clavier et consacré son temps à donner son avis éclairé.
Il me semble que l’on avance, tout doucement, vers le dénouement.
CQFD ? : Pas tout à fait encore ! … :
Jusque-là, personne n’avait imposé les qualificatifs
d’Actuariel et Continu au Taux d’Inflation.
Et tout est, effectivement, affaire de définition, y compris celle du
domaine d’application.
Car si j’ai déjà entendu parler, plus ou moins couramment, de divers
Taux en fonction de la période retenue : Journalier, Hebdomadaire, Mensuel,
Trimestriel, Semestriel, Annuel, Biannuel, Décennal, …, je ne sache
pas que pour le Taux d’Inflation de l’Indice des Prix à la
Consommation, lorsqu’on évoque les Années 0, 1, 2, …, 1998,
1999, 2000, 2001, 2002, …, 2008, 2009, 2010, 2011, 2012, 2013, 2014,
…, n-1, n, n+1, …, ces dernières puissent être autres
qu’Entières.
Je n’ai jamais entendu parler, à ce sujet, d’Année
Fractionnaire (Année 2014 10/12), Décimale (Année 2014.83…), ni
Réelle (Année 6 329,785598…/Pi) !
Dans l’énoncé du problème, on peut lire :
"En effet si l'inflation était constante, au bout de n années, l'IPC serait
de IPC année 1 x (1+inflation)^n avec n>1, nous aurions une parabole."
Or, en reprenant les notations précédemment exposées, avec un Taux
d’Inflation Annuel Constant, égal au Taux Initial, t0, et en
considérant bien, comme périodes, des Années Entières (de 365 ou 366 jours,
peu importe d’ailleurs, puisque la plupart du temps seuls 360 sont
pris en compte, toujours par définition et convention, même si c’est
par facilité !), avec n>0, on peut écrire les valeurs successives
annuelles de l’IPC sous la forme :
IPC1=IPC0.(1+t0)
IPC2=IPC1.(1+t0)
.
.
.
IPCn=IPC(n-1).(1+t0)
Par addition membre à membre et simplification, on obtient :
IPCn=IPC0.(1+t0)^n : (A)
On retrouve bien la formule de l’énoncé (dont la courbe, ceci dit en
passant, n’a rien d’une parabole, contrairement à
l’affirmation, mais ce n’est pas le sujet ! …)
Cette dernière formule correspond donc bien au problème posé, nous sommes
dans son domaine d’application !
Le raisonnement, pour obtenir une courbe annuelle Linéaire de l’IPC,
donc une différence constante ΔIPC de l’IPC d’une Année
par rapport à celui de l’Année précédente, nous a conduits à écrire
la formule :
IPCn=IPC(n-1)+ΔIPC : (B)
Pour le problème posé et les hypothèses prises en exemple (IPC0=100, t0=2%
et donc, on l’a vu : ΔIPC=2), il résulte la suite des IPCn, à
savoir :
IPC0=100, IPC1=102, IPC2=104, IPC3=106, IPC4=108, IPC5=110, IPC6=112,
IPC7=114, IPC8=116, IPC9=118, IPC10=120.
Ces valeurs, évidentes, sont corroborées, sans contradiction ni preuve du
contraire pour l’instant, par la formule hyperbolique proposée pour
le Taux d’Inflation :
tn=t0/(1+n.t0) :(C)
On peut décider de qualifier de "Discontinu" ce Taux d’Inflation
Annuel, tn, au regard du fait qu’il s’applique à des Années
Entières (au sens mathématique du terme), il me semble que, malgré tout,
c’est celui qui est implicitement demandé.
Avec ce tn, variable en fonction de n, entier, on a bien :
IPC1=IPC0.(1+t0)=100.(1+2%)=102
IPC2=IPC1.(1+t1)=IPC1.(1+t0/(1+1.t0))=102.(1+2%/(1+1x2%))=104
Etc.
Sincères salutations.
mathématicien
02 Oct. 2014, 22:24
En mathématique, comme dans d'autres domaines, tout est affaire de
définition...
Voici donc un nouveau tableau comparatif avec des valeurs arrondies, cette
fois, à 3 décimales:
0 2,000% 100,00
1 1,980% 102,00 2,000%
2 1,961% 104,00 1,961%
3 1,942% 106,00 1,923%
4 1,924% 108,00 1,887%
5 1,906% 110,00 1,852%
6 1,889% 112,00 1,818%
7 1,872% 114,00 1,786%
8 1,855% 116,00 1,754%
9 1,839% 118,00 1,724%
10 1,823% 120,00 1,695%
En fait les 2 colonnes de pourcentages sont différentes car elles ne
signifient tout simplement pas la même chose!
La 1ère colonne, calculée avec la formule taux=ln(1 + 2%*année)/année,
correspond à un taux actuariel CONTINU.
En faisant le rapport Vn/Vn+1 entre 2 années successives, on obtient alors
les résultats "hyperboliques" mentionnés précédemment mais dans ce cas il
s'agit d'un taux annuel donc DISCONTINU.
Ceci explique que les 2 colonnes contiennent des valeurs différentes.
CQFD?
IPC Linéaire 3
02 Oct. 2014, 11:42
Bien le bonjour.
Voici la démonstration, par le détail, de la formule hyperbolique proposée,
tn=t0/(1+n.t0), pour une variation linéaire de l’Indice des Prix à la
Consommation IPCn :
1) Notations :
n=Année n
IPCn=Indice des Prix à la Consommation au début de l’Année n
tn=Taux d’Inflation (%) au cours de l’Année n
2) Hypothèses :
0=Année de base
IPC0=100=Indice au début de l'Année de base
t0=2%=Taux d'Inflation au cours de l'année de base
ΔIPC=IPC(n+1)-IPCn=2 : variation, supposée constante, de
l’Indice d’une Année n à la suivante n+1.
3) Démonstration :
On peut écrire les lignes suivantes :
IPC1=IPC0+ΔIPC
IPC2=IPC1+ΔIPC
.
.
.
IPC(n-1)=IPC(n-2)+ΔIPC
IPCn=IPC(n-1)+ΔIPC
Et par addition de toutes ces lignes, membre à membre, et simplifications,
il vient :
IPCn=IPC0+n.ΔIPC
Or, par hypothèse IPC0 et ΔIPC sont chacun différent de 0, donc
IPCn#0.
Par ailleurs :
on a
IPC(n+1)=IPCn.(1+tn) soit, puisque IPCn#0 :
IPC(n+1)/IPCn=1+tn, qui, d’une part, donne
tn=IPC(n+1)/IPCn-1 : (1)
et on a aussi
IPC(n+1)=IPCn+ΔIPC :
D’où :
IPCn+ΔIPC=IPCn.(1+tn)=IPCn+IPCn.tn
Et, en supprimant IPCn, membre à membre, il reste :
ΔIPC=IPCn.tn (en particulier, pour n=0, ΔIPC=IPC0.t0, que nous
utiliserons plus loin !), et donc, d’autre part :
tn=ΔIPC/IPCn : (2) puisque IPCn#0.
(pour n=0 et n=1, on retrouve bien, respectivement, les t0=ΔIPC/IPC0
et t1=ΔIPC/IPC1 déjà déterminés antérieurement)
D’où :
tn=ΔIPC/(IPC0+n.ΔIPC)
tn=IPC0.t0/(IPC0+n.IPC0.t0) et,
en simplifiant par IPC0 (différent de 0), on obtient, enfin, la formule si
convoitée :
tn=t0/(1+n.t0) : (3) ; CQFD
4) Résultats pour l’exemple :
Les séquences des chiffres décimaux se répètent indéfiniment.
n IPCn tn=t0/(1+n.t0)=ΔIPC/IPCn=IPCn+1/IPCn-1(en %)
0 100 2
1 102 1.960 784 313 725 490 1…
2 104 1.923 076…
3 106 1.886 792 452 283 01…
4 108 1.851…
5 110 1.81…
6 112 1.785 714 2…
7 114 1.754 385 964 912 280 701…
8 116 1.724 137 931 034 482 758 620 689 655 1…
9 118 1.694 915 254 237 288 135 593 220 338 983
050 847 457 627 118 644 067 796 610 1…
10 120 1.6…
. . .
. . .
. . .
Et, pour faire plaisir à Mathématicien :
100 300 0.6…
pour n tendant vers l'infini, IPCn tend vers l'infini et tn tend vers 0.
Sincères salutations.
IPC Linéaire 2
28 Sep. 2014, 18:17
Bien le bonjour.
Il semble bien difficile à tout un chacun de reconnaitre ses erreurs !
J’essaie donc de simplifier encore pour démontrer l’erreur de
raisonnement de mathématicien :
Hypothèses :
IPC0 : Indice des Prix à la Consommation au début de l’Année 0 de
base ; égal à 100 comme base.
t0 : Taux d’Inflation au cours de l’Année 0 ; égal à 2%.
Raisonnement :
IPC1 : Indice des Prix à la Consommation au début de l’Année 1 :
IPC1=IPC0(1+t0)=100(1+2%)=100(1+2/100) =100+100(2/100)=100+2=102.
D’où la différence d’indices pour la première année :
ΔIPC=IPC1-IPC0=102-100=2.
En conservant la différence ΔIPC constante pour les années suivantes
(ce qui est l’hypothèse de l’exercice) on obtient :
IPC2=IPC1+ΔIPC=102+2=104 au début de l’Année 2, avec
IPC2=IPC1(1+t1)
Or, si t1, le Taux d’Inflation au cours de la deuxième année avait,
lui aussi, été égal à 2%,
l’Indice des Prix à la Consommation au début de l’Année 2
aurait été égal à 102(1+2%)=102+2.04=104.04.
Cette valeur est effectivement différente de 104, même si c’est de
très peu : 0.04 !
Sauf si évidemment on arrondissait ? ... Ce qui fausserait le raisonnement
!
C’est d’ailleurs ce qui est exposé dans l’énoncé du
problème.
Jusque-là, il me semble que tout le monde devrait être d’accord !
Il convient donc que le Taux d’Inflation de l’Année 2 (et aussi
des suivantes) soit différent de 2% et d’ailleurs inférieur à cette
valeur.
Et là commence les divergences de raisonnements pour la détermination de la
formule de son calcul et donc des résultats !
Et pourtant, d’après :
ΔIPC=IPC1-IPC0 et IPC1=IPC0(1+t0), on a
ΔIPC=IPC0(1+t0)-IPC0=IPC0+IPC0.t0-IPC0.
Il est donc facile de démontrer que le Taux d’Inflation au cours de
la première année est égal à :
t0=ΔIPC/IPC0=2/100=2%, ce qui par ailleurs était une évidence !
Par un raisonnement semblable, d’après :
IPC2=IPC1+ΔIPC et IPC2=IPC1(1+t1), on a :
IPC1+ΔIPC=IPC1(1+t1)=IPC1+IPC1.t1, d’où
ΔIPC=IPC1.t1
On obtient donc, aussi évidemment, le Taux d’Inflation de la deuxième
année qui est égal à :
t1=ΔIPC/IPC1=2/102=1.960 784 313 725 490 1…%
(la séquence des 16 chiffres décimaux se répétant indéfiniment)
t1, dans le tableau du 14/05/2014, avait été arrondi, en affichage
seulement comme précisé,
à 4 chiffres derrière le virgule, d’où la valeur mentionnée de
1.9608...
Et, si tous les chiffres significatifs derrière la virgule sont bien pris
en compte, on peut vérifier que :
IPC2=IPC1(1+t1)=102(1+1.960 784 313 725 490 1…%)=104, exactement
… !
Quelle que soit la formule ou la fonction retenue pour déterminer le Taux
d’Inflation d’une année, le résultat doit rester celui-ci.
Or il est bien évident qu’avec la valeur trouvée par mathématicien
(1.98% !), il n’en est rien puisqu’on arrive à 104.0196.
Cette valeur est fausse et les suivantes aussi ! Par exemple celle de la
10ème année est erronée de plus de 8%.
Ces résultats devraient inciter mathématicien à se remettre en question,
mais il a décidé que sa contribution du 22 courant était la dernière.
Il ne sert à rien de se projeter dans 100 ans, ou pire à l’infini
dans le futur, (c’est bien loin tout ça)
si on ne peut justifier sa position de manière exacte pour dans quelques
années, voire seulement à un an ou deux.
Comment se défendre auprès des banquiers avec de tels arguments ?
(Planer à 10 000m d’altitude permet aussi d’avoir une vision
d’ensemble, mais avec la contrepartie, du coup, de ne plus pouvoir
déceler le détail)
Ce n’est pas parce qu’une courbe se rapproche à l’infini
d’une droite donnée, qu’à l’origine ou ailleurs elle
n’en est pas excessivement, voire infiniment, éloignée.
Et d’autres courbes, différentes, donc donnant des résultats
différents, peuvent avoir cette même droite comme asymptote.
Où peut bien être la faille dans mon raisonnement : dommage que
mathématicien ne me l’ait pas explicitée.
Personnellement j’aurais été ravi de la connaitre, si elle existe
bien sûr, et je l’en aurais remercié en me remettant en cause.
Pour l’instant, et jusqu’à preuve du contraire je reste sur la
fonction hyperbolique tn=t0/(1+n.t0), qui, pour t0=2%,
donne les valeurs consécutives portées au tableau du 14/05/2014.
Sincères salutations.
mathématicien
22 Sep. 2014, 21:43
Voici ma dernière contribution au problème "IPC linéaire" afin de répondre
de manière la plus claire possible au message du 14 Mai 2014.
L'utilisation de la fonction logarithme népérien permet de calculer de
manière exacte le taux actuariel t i.e. le paramètre de la fonction
exponentielle qui permet le calcul de la valeur V(x) en fonction de V(0),
du taux d'intérêt t et de la durée x: V(x)=V(0).exp(t.x).
Pourquoi la fonction exponentielle?
Et bien parce que la fonction (1+t/n)^n, utilisée pour connaitre la valeur
V(n) dans le cas d'intérêts composés, tend vers la fonction exp(t) quand n
tend vers l'infini, cad, quand la période utilisée pour calculer tend vers
0. En quelque sorte la fonction exponentielle est une loi limite et permet
de trouver "facilement" le taux t en prenant le logarithme (fonction
inverse de la fonction exp) de V(x).
La formule donnée le 01 juin 2013 a été déterminée par cette méthode en
considérant une évolution linéaire de l'IPC de 2% pour une période n.
Pour finir et pour illustrer la différence entre une évolution linéaire et
une évolution exponentielle voici les valeurs calculées de l'IPC (base 100)
dans les 2 cas au bout de 100 ans:
Evolution linéaire: V(200) = 300 (100 + 2% * 100)
Evolution exponentielle : V'(200) = 738,91 (2,46 x plus!)
Jean
20 Août 2014, 18:46
Bonjour,
Pensez-vous que nous allons avoir une déflation, comme le prédisent en ce
moment de nombreux commentateurs ? La dynamique
article ici
est-elle vraiment engagée ?
Merci
Jean
Jean
20 Août 2014, 18:42
Bonjour,
Pensez-vous que nous allons avoir une déflation, comme le prédisent en ce
moment de nombreux commentateurs ? La dynamique est-elle vraiment engagée
?
Merci
Jean
article ici
IPC Linéaire
14 Mai 2014, 14:24
Bien le bonjour à tous,
Suite aux commentaires trouvés sur le site "france-inflation.com",
concernant la formule de variation du Taux d’Inflation nécessaire
pour obtenir une évolution linéaire de l’Indice des Prix à la
Consommation (IPC), il me semble que le problème est mal posé et les
solutions proposées erronées.
Prenons les Hypothèses suivantes pour simplifier le raisonnement :
n : Année considérée (0 de Base, 1, 2, 3,…) ;
IPC(0) : Indice des Prix à la Consommation de l’Année 0
=Base
=100 ;
IPC(n) : Indice des Prix à la Consommation de l’Année n>0 ;
ΔIPC : Évolution annuelle supposée constante de la courbe de
l’IPC (droite)
=IPC(n)-IPC(n-1)
=2
soit IPC(n)=IPC(n-1)+ΔIPC
=IPC(n-1)+2
et par récurrence :
=IPC(0)+n.ΔIPC
=IPC(0)+2n
=100+2n ;
t0 : Taux d’Inflation au cours de l’Année 0 en %
=ΔIPC/IPC(0)
=2/100
=2% ;
tn : Taux d’Inflation au cours de l’Année n>0 en %
={IPC(n+1)/IPC(n)–1}
={IPC(n+1)–IPC(n)}/IPC(n)
=ΔIPC/IPC(n)
=ΔIPC/(100+2n)
=2/(100+2n) ;
et les valeurs arrondies par mathématicien :
IPC(n)~ : Indice des Prix à la Consommation de l’Année n,
arrondis à l’unité ;
tn~ : Taux d’Inflation au cours de l’Année n,
arrondis à 2 décimales ;
Avec ΔIPC=2, on peut dresser le tableau comparatif suivant :
IPC Linéaire mathématicien
14 Mars 2014 05 Déc.2013,21:13
n IPC(n) tn en % IPC(n)~ tn~
0 100 2.0000… 100.00 2.00%
1 102 1.9608… 102.00 1.98%
2 104 1.9231… 104.00 1.96%
3 106 1.8868… 106.00 1.94%
4 108 1.8519… 108.00 1.92%
5 110 1.8182… 110.00 1.91%
6 112 1.7857… 112.00 1.89%
7 114 1.7544… 114.00 1.87%
8 116 1.7241… 116.00 1.86%
9 118 1.6949… 118.00 1.84%
10 120 1.6667… 120.00 1.82%
L’augmentation annuelle ΔIPC de l’IPC étant égale à 2, il
est à remarquer que si on peut bien parler d’une Inflation, au cours
de l’Année 0 de Base 100 (valeur initiale), d’un Taux t0 de 2%
(=2/100), il n’en est pas de même pour les Années suivantes car leur
propre valeur initiale n’est plus égale à 100.
C’est en cela que le problème me semble mal posé dans les phrases
suivantes :
"La tendance de l'IPC est représentée par la droite en pointillé dont la
pente est de 2% … ;
L'indice des prix suit une droite de pente 2% …"
car en fait, la pente n’est pas de 2% mais de 2/Année (=ΔIPC sur
1 Année) ! …
Dans le tableau, la différence ΔIPC=IPC(n)-IPC(n-1) est bien, par
hypothèse, exactement égale à 2, c’est-à-dire à l’augmentation
annuelle, supposée constante, de l’IPC.
Les valeurs des IPC(n) de la colonne 2 et des tn de la colonne 3 sont
exactes (même si ces dernières sont affichées arrondies à la 4ème décimale
seulement), alors que à celles des IPC(n)~ de la colonne 4 et des tn~ de la
colonne 5 sont arrondies par mathématicien.
La linéarité souhaitée de la courbe des IPC(n) est de ce fait vérifiée.
C'est la seule véritable droite.
La linéarité de la courbe des IPC(n)~ n’est, en fait,
qu’apparente ! ...
Au lieu de la fonction logarithmique népérienne tn~=arrondi{ln(1+n.t0)/n;4}
avec IPC(n)~ arrondi à l’unité, utilisée par mathématicien, je
propose aux différents contributeurs de retenir la fonction hyperbolique
suivante, sans arrondis et relativement plus simple : tn=t0/(1+n.t0)
Dans les 2 cas, quand n tend vers l’infini, tn tend vers 0, mais à
des vitesses différentes. En comparant les valeurs (et pourquoi pas les
courbes !) de ces 2 fonctions, on voit apparaître leur divergence.
L’apparente linéarité de la courbe mentionnée dans le commentaire du
05/12/2013 est due à l’utilisation de la fonction logarithmique (qui
"écrase") et des arrondis (qui "trompent")
Dans les IPC(n)~, les 2 zéros derrière la virgule y sont systématiquement
faux. Malgré les décimales, ces IPC(n)~ se révèlent en fait "arrondis" à
l’unité.
Dans les tn~, les arrondis à seulement 2 chiffres décimaux significatifs
sont abusifs et impactent les résultats.
En fait, on cumule les erreurs de calculs et du coup le jugement est faussé
!
Avec des calculs exacts la linéarité de l’IPCn~ n’est pas
obtenue.
On le voit bien par la divergence entre les valeurs erronées des tn~ et
celles exactes des tn aboutissant, elles, à une véritable linéarité de
l’IPC.
Aussi, il n’est pas nécessaire de passer par une fonction
logarithmique, même népérienne. Elle est fausse dans l’absolu de
toute façon.
Quant à Rectif, si je partage ses ressentiments à propos de
l’exploitation de ces indices, je crois pouvoir lui dire que si
"L'inflation est l'évolution de l'indice de la période considérée par
rapport à celui de la période précédente", l’utilisation de sa
formule du 12 Nov. 2013 concernant l’Inflation I(n)=IPC(n)/IPC(n-1)
me semble aussi inappropriée, car l’Inflation ne se mesure
apparemment pas simplement par le quotient de 2 indices successifs de
l’IPC mais par le Taux d’Inflation au cours de la Période p :
tp={IPC(p+1)/IPC(p)–1)
={IPC(p+1)–IPC(p)}/IPC(p)
=ΔIPC(p)/IPC(p)
Espérant avoir contribué au mieux et sans erreur à la résolution du
problème posé, sans animosité, et avec mes sincères salutations à tous
…
Tracfinn
07 Fév. 2014, 12:04
Petite erreur dans l'interprétation du coefficient de régression de otre
article : ce dernier donne bien le taux mensuel, néanmoins le taux annuel
n'est pas donné par la formule Iannuel = (1 + Imensuel x 12) - 1
Mais par la formule : Iannuel = (1 + Imensuel)^12 - 1
Ce n'est pas grand chose, on arrive toujours à +2% par an mais sur de plus
longues périodes ou pour des calculs plus méticuleux, ça peut avoir son
importance. Je ne jette pas la pierre : les banques font l'erreur depuis
des années sur leurs prêts.
Réponse le 7/2/2014
Ce n'est pas la première fois que cette remarque est faite, et je
réexplique bien volontier:
L'inflation annuelle est bien égale à la moyenne des 12 inflations
mensuelles : (1 + Imensuel x 12) - 1.
Et ceci en fait par convention (site Insee) !
Donc la formule normale des taux composés Iannuel = (1 + Imensuel)^12 - 1
ne s'applique pas ici.
Je ne connais pas vraiment l'origine de ce choix, probablement par
simplification.
Vous pourrez remarquer que le même choix a été fait pour les intérêts du
Livret A : le taux de chaque quinzaine est égal au taux annuel divisé par
24 et n'est donc pas égal au taux plus exact donné par les taux composés
(1+i)^(1/24) !!
Par contre, quand on passe à la maille annuelle, là les taux composés
reprennent leur droit.
Cordialement
Daour
01 Fév. 2014, 16:17
Je dois monter un budget, j'ai les données de 2012 bien établies. Pour les
achats,si je considère une inflation de 3% pour l'année 2013 et 2014,
biaiserai je mes résultats?
Merci
Réponse du 7/2/2014
L'inflation moyenne de 2013 a été de 0.9%
La prévision pour 2014 est de 1.4%
Sur les deux années, cela fait donc 1.009*1.014= 1.023 soit 2.3%
d'inflation.
Si vous considérez 3% cela est donc légèrement supérieur, vous avez une
marge.
Maintenant, il se peut que votre budget n'ai pas la même structure que le
panier Insee, il faudrait faire un test sur le site de l'insee pour être
plus précis
Simuler un indice personnalisé
Par exemple, si vous fumez, votre budget tabac va représenter plus des
2.06% que considère l'insee ( c'est la moyenne entre tous les Français,
donc fumeurs et non fumeurs) et comme les tabacs ont augmentés de 6.8% en
2013, votre inflation individuelle var être supérieure aux 0.9% moyens de
2013.
Rectif
17 Déc. 2013, 14:50
@mathématicien:
effectivement, mais la conclusion essentielle pour moi est qu'on utilise
l'inflation pour duper les gens. Exemple : l'augmentation du SMIC
supérieure à l'inflation donc une augmentation du pouvoir d'achat pour les
personnes concernées. C'est faux. La revalorisation du SMIC est calculée
par comparaison à l'année en cours, l'inflation par rapport à l'année 2000.
Sans parler de l'amalgame qui est volontairement fait entre l'inflation
courante et la moyenne annuelle.
mathématicien
05 Déc. 2013, 21:13
Simulation de l'évolution de l'IPC avec la fonction taux=ln(1 +
2%*année)/année indiquée en juin.
L'évolution de l'IPC est bien linéaire.
année taux IPC (année)
0 2,00% 100,00
1 1,98% 102,00
2 1,96% 104,00
3 1,94% 106,00
4 1,92% 108,00
5 1,91% 110,00
6 1,89% 112,00
7 1,87% 114,00
8 1,86% 116,00
9 1,84% 118,00
10 1,82% 120,00
Rectif
12 Nov. 2013, 11:44
Correction du commentaire précédent :
I(n)= 1 + 1/[IPC_2000/delta + (n-1)]
Mais la définition de l'inflation (en gras dans l'article) pour aboutir à
ce résultat est fausse : l'inflation n'est pas simplement le ratio de l'IPC
d'une année sur l'autre, mais plutôt le ratio de la variation d'IPC sur la
valeur de l'année précédente, soit :
INF(n)=[IPC(n)-IPC(n-1)]/IPC(n-1)=I(n)-1
et donc INF(n)=1/[IPC_2000/delta + (n-1)] qui tend vers 0 avec le temps qui
passe. Pour être plus représentaif, il faudrait diviser l'écart par quelque
chose de fixe, comme la valeur de référence IPC_2000, et non par quelque
chose qui augmente d'année en année.
L'inflation n'est vraiment pas le bon outil pour chiffrer l'augmentation du
coût de la vie ! C'est un indicateur complètement biaisé en fonction du
choix de l'année de référence.
Rectif
12 Nov. 2013, 10:57
Je crois que la réponse à la question posée aux mathématiciens (bien que je
n'en sois pas un) est quelque peu différente de celle déjà apportée en juin
dernier.
Si l'augmentation de l'IPC est constante alors :
IPC(n)=IPC(n-1)+delta où pour faire simple n est le nombre d'années écoulée
depuis 2000, et delta=12*0.1636=0.1932 l'augmentation d'une année.
l'inflation I est le rapport de l'IPC d'une année à l'autre, donc
I(n)=IPC(n)/IPC(n-1)
On peut donc écrire l'IPC(n) de deux façon:
IPC(n)=IPC(n-1)+delta
IPC(n)=I(n)*IPC(n-1)
en remplaçant IPC(n-1) issu de la première équation dans la seconde, on
obtient:
IPC(n)=I(n)*[IPC(n)-delta]
soit I(n)=IPC(n)/[IPC(n)-delta]
Connaissant la valeur de l'IPC à une date (IPC_2000=101.2)
on sort IPC(n)=IPC_2000 + n*delta et donc la valeur de l'inflation n année
après l'an 2000:
I(n)=[IPC_2000 + n*delta]/[IPC_2000 + (n-1)*delta]
A noter qu'on peut aussi l'écrire :
I(n)= 1 + 1/[IPC_2000/delta + (n-1)*delta]
soit 1 plus quelque chose qui tend vers 0. Si l'on suit cette évolution,
les prix continuent de grimper linéairement, et l'inflation tend vers 1.